北海道大学クラーク会館大講堂 オルガン3.パイプの長さ・太さ・パイプと振動数
一番単純なのはAのような 振動です。 この振動では、 ある時には点線の状態だった空気が、 次には実線の状態になっています。 管の両端の空気は自由に振動し、 一方真ん中の部分(→)は時間が経っても動きません。 図のBのような 振動も可能です。 この振動では、管の両端や真ん中の空気は自由に振動しますが、 管の中に二ヶ所、 時間がたっても空気が振動しない場所(→)があります。
さらに図のCのような振動も作れます。
今度は空気の振動しない場所(→)が三ヶ所あります。
同様にして色々な振動を作ることが出来ます。
AとBとCでは振動数の比は1:2:3である、と言えます。
振動数が高いほど音の高さも高くなります。
・倍音と音色
2.ドとその上のソは振動数比が2:3
同様に、2.を用いれば、 BとC の振動数の比は2:3なので、
結局、
この管では
振動 Aが与える
基準のド
の上に、
一オクターブ高い
ド(振動数２倍)
が振動Bによって、
さらに、
その上の
ソ(振動数３倍)
が振動Cによって
実現することが分かります。
この様子を楽譜に書くと右上のようになります。
ここまで見て来たような様々な振動が、実際には 上のEのように同時に実現しています。 ここには振動数が３倍のものまで描かれていますが、 現実には振動数が４倍、５倍…の音も鳴るのです。 Aのような 振動数の基準になる音を基音、 これに対して振動数が２倍、３倍の音を倍音と言います。 私達が色んな楽器でドの音を鳴らした場合は、 その音を基音として様々な倍音が含まれているのです。 色々な倍音の多様な含まれ方は音の表情(音色) となって耳に伝わります。 オルガンには同じドの音を出すのに、 色々な音色のパイプがあります。 この 音色の違いは、 パイプの種類による倍音の含まれ方の違いからくるのです。 オルガンに限らず、 同じ振動数440Hz(ラ)の音を出した時に色々な楽器からのラの音の音色が 違うことはやはり倍音の含まれ方の違いから生じるのです。 パイプオルガンの場合、
ということが知られています。 またオルガンの演奏者は、 特定の倍音のストップを入れることで、 倍音を強めたることが可能です。 これによって音色に変化を付けることが出来ます。 ストップの組み合わせとは、 言い替えれば倍音の割合を色々に調合して音色を作ること、 とも言えます。 またそれぞれの倍音の役割については、 以下のように書いてある論文があるようです。
・パイプの長さと音の高さ
同様に、 パイプAの振動数３倍の倍音(ソ)の振動 (水色の振動 を基音とするようなパイプ(パイプJ)を作ると、 このパイプJは、 パイプIのドの上のソを鳴らすことになります。 長さはAの３分の１で、2 2/3フィートです。 このようにパイプの長さを変えることで色んな高さの音のパイプを 作ることが出来ます。 ここまでのことからパイプオルガンの場合、
短いパイプ：高い音 が出ることが分かりました。
さて、このようにしてドやソのパイプを作ることが
出来ました。
同様のことを繰り返せば、
ドとソについては、あらゆる高さの音のパイプを
どの長さにすれば良いかが分かります。
例えば、
Aの一オクターブ低いドを作るには、
長さをAの２倍、16フィートにすれば良いし、
Iのさらに一オクターブ高いドを作るには、
長さをIの半分、2フィートにすれば良いのです。
また、Jの一オクターブ高いソを作るには、
長さをJの半分、1 1/3フィートにすれば良いのです。
この節で出て来た長さは、オルガンを弾く人には耳に馴染みがあるでしょう。
・様々な倍音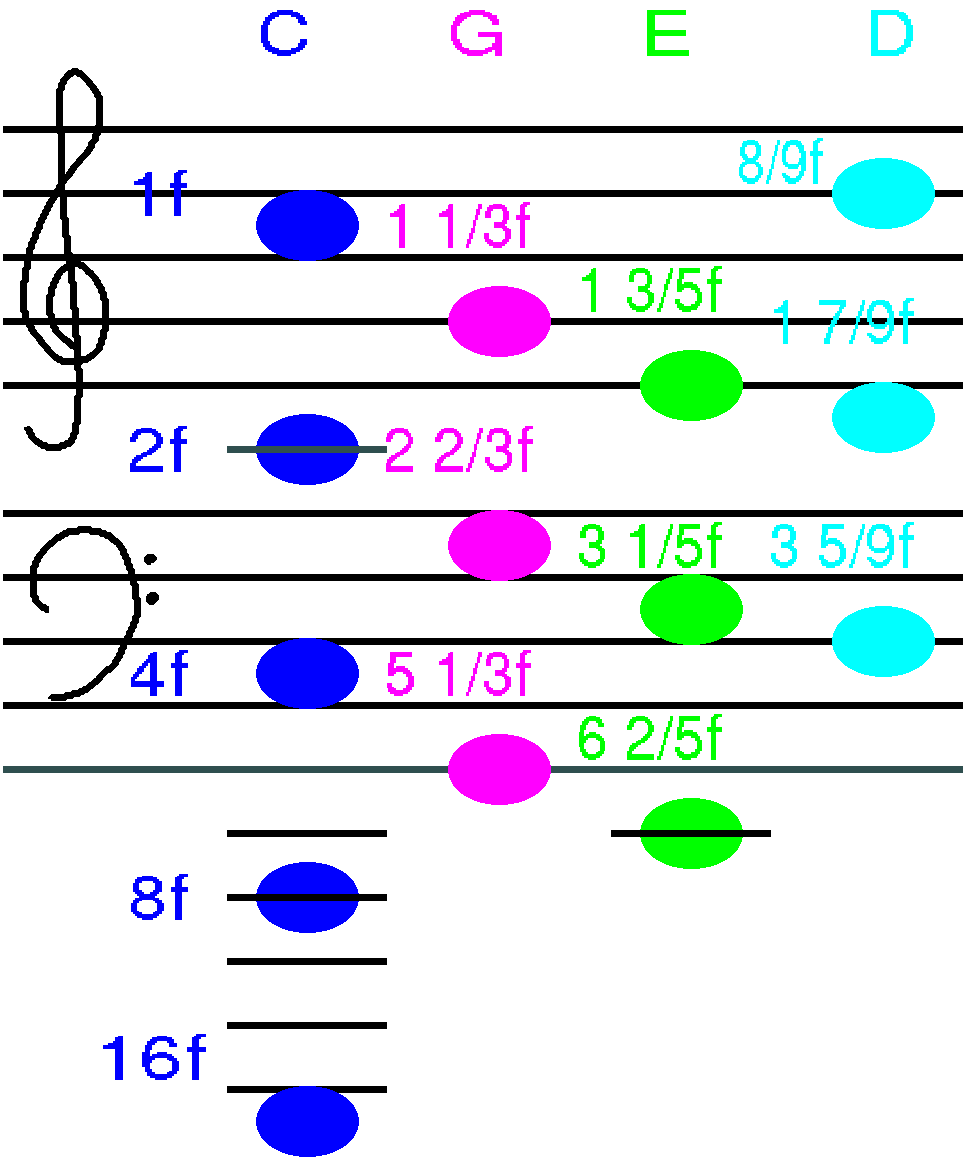
3.ミとその上のドは振動数比が5:8 4.レとその上のドは振動数比が8:9 この法則と先に述べた法則、
1.ドとそのオクターブ高いドは振動数比が1:2 を用いると図のように色々な高さのドレミソの管の長さが 決まります。どの２つの音の関係もこれらの法則で関係 付けられるが分かります (振動数とパイプの長さは反比例の関係であることに注意、 例えば、振動数の比が2:3なら、管の長さの比は3:2)。
ドに限らずいずれのオクターブの関係もパイプの長さの比1:2、
ソとその上のレはパイプの長さの比3:5(ドとその上のソの関係と同じ)
であることなどが分かります。
・ストップへの数字の表示
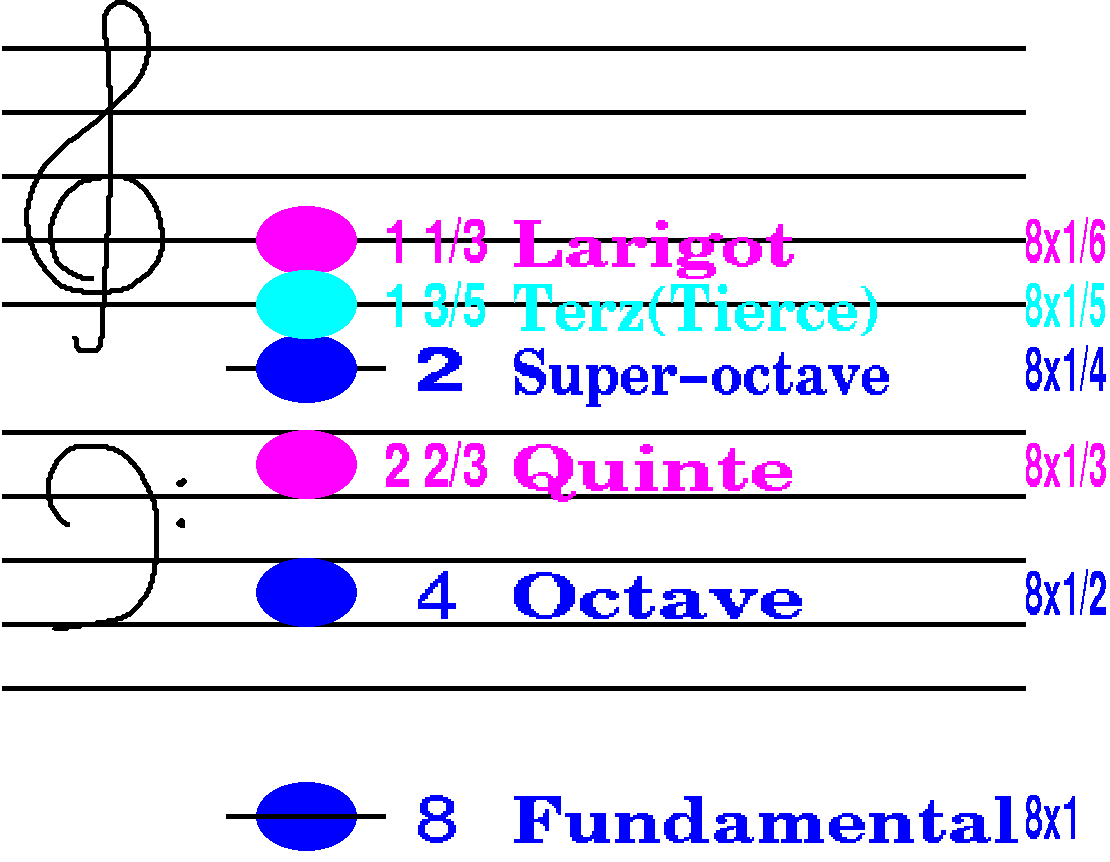
例えば、 7.Prinzipal 8' というストップを入れて鍵盤の一番下のドを鳴らすと、 8フィートの長さのパイプが鳴ります。 楽譜に示すとこの音はドの音です。 これに対して、 9.Octav 4'というストップを入れて 鍵盤の一番下の下のドを鳴らすと、 Octavに属するパイプのうち 4フィートの長さのパイプが 鳴ります。 楽譜に示されたように、 一オクターブ、二オクターブ高いドの音が鳴ることになります。 このように、8'のストップとオクターブの関係にある音を鳴らすストップを、 オクターブストップと言います。 また、このように基音に対してオクターブの関係にある倍音のことを 偶数倍音と言います。 例えば、 第2倍音(Octave)、第4倍音(Super-octave) は偶数倍音です。 また、基音に対してオクターブ以外の関係にある倍音のことを 奇数倍音と言います。 例えば、 第3倍音(Twelfth)、第5倍音(Tierce)、第6倍音(Larigot) は奇数倍音です。
北大オルガンのストップに登場する各フィートに属するパイプを 最低のドの鍵盤で弾いた時に実際に鳴る音を示したのが 上の図です。 音符の横には、ストップに表示されるフィート数、名称を示し、 さらにパイプの長さが下から1/2,1/3,…となっていることを示しました。 振動数の言葉で言えば、基音に対して第６倍音に対応する音まで書かれて いることになります。
・開管と閉管
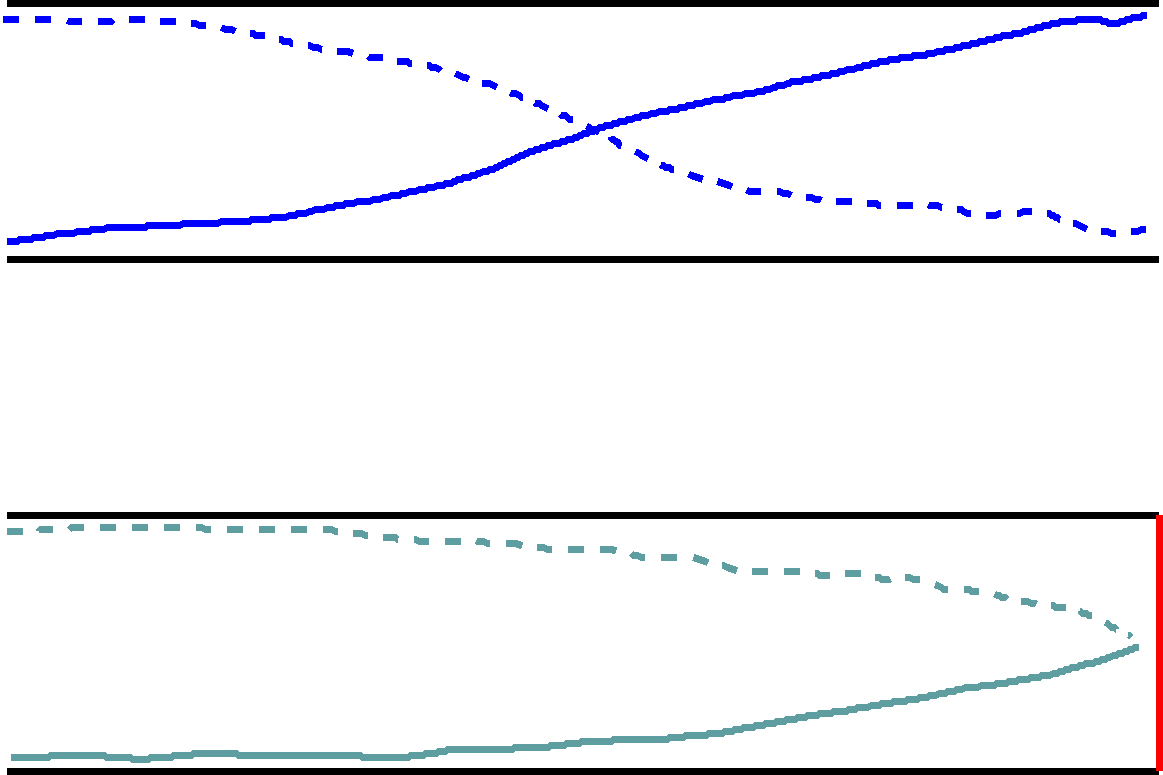ここまでは管の両端の空いた管を考えました。
これを開管と言います。
最後に、ここでは片方の端を閉じた管(閉管)
を考えて見ましょう。
同じ管の長さで開管と閉管を比べると事情がどのように変わるでしょうか。
基音を比べてみましょう。
左図を見て下さい。
半さつま2個が入った開管の基音と比べると
閉管の基音には(2倍の長さの)半さつまが1個だけ入っている
ことに気づきます。
これは閉管では片方の端では空気が動くことが出来ず常に固定される
ことから生じる違いです。
振動数の言葉で言えば、
閉管の基音の振動数は開管の基音の振動数の2倍である
ことになります。パイプの長さの言葉で言えば、
ある長さの管を用意した時に閉管が与える基音は、
同じ長さの開管の与える基音の1オクターブ低い
ということになります。
開管であるPrinzipal 8'に属するある長さのパイプの音と 閉管であるHolz gedackt 8'に属する同じ長さのパイプの音を 比べるとHolz gedackt 8'が与える音の方が一オクターブ低くなります。
実はこの規則は開管についてのものです。 閉管の場合、最低のドの鍵盤を鳴らした時に音を出すパイプの長さの 長さの2倍がストップに表示されます。 このことにより、 開管閉管に関わらず、 ストップに書かれた数字が同じなら 音の高さは同じ であることになります。パイプの長さとストップ表示の 規則を厳密に書けば、ストップに表示される管の長さは、
閉管ストップ：鍵盤の一番低いドの音を弾いた時に実際に鳴るパイプの長さの２倍を表示
となります。
・まとめ
・物理を知っている人に簡単な例題
解
である。 両端が空いたパイプの場合、 パイプの長さの2倍が基音の波長に相当する (このページの一番上の図を参照)。 だから、 この波長を基音とするパイプの長さは、
このパイプを2倍の長さにする作業を3回行って、 パイプの長さを元の8倍、2.532mとすると、 この値は8フィートに近い。 音としては523Hzのドに対して3オクターブ低いドの音となる。 だから8フィート管の8フィート位の長さの管は、 この問題ではおおよそ2.53mである。 実際には時代・場所によってピッチは変化しているので、 この長さもまちまちである。 例えば、 北ドイツの17世紀のコーアトーンと呼ばれる高さは現在の一般的な 調律より全音高い(パイプの長さが一音分、短い)。 北大オルガン研のホームページへ 更新：1999.10.31 製作：北大オルガン研究会 |
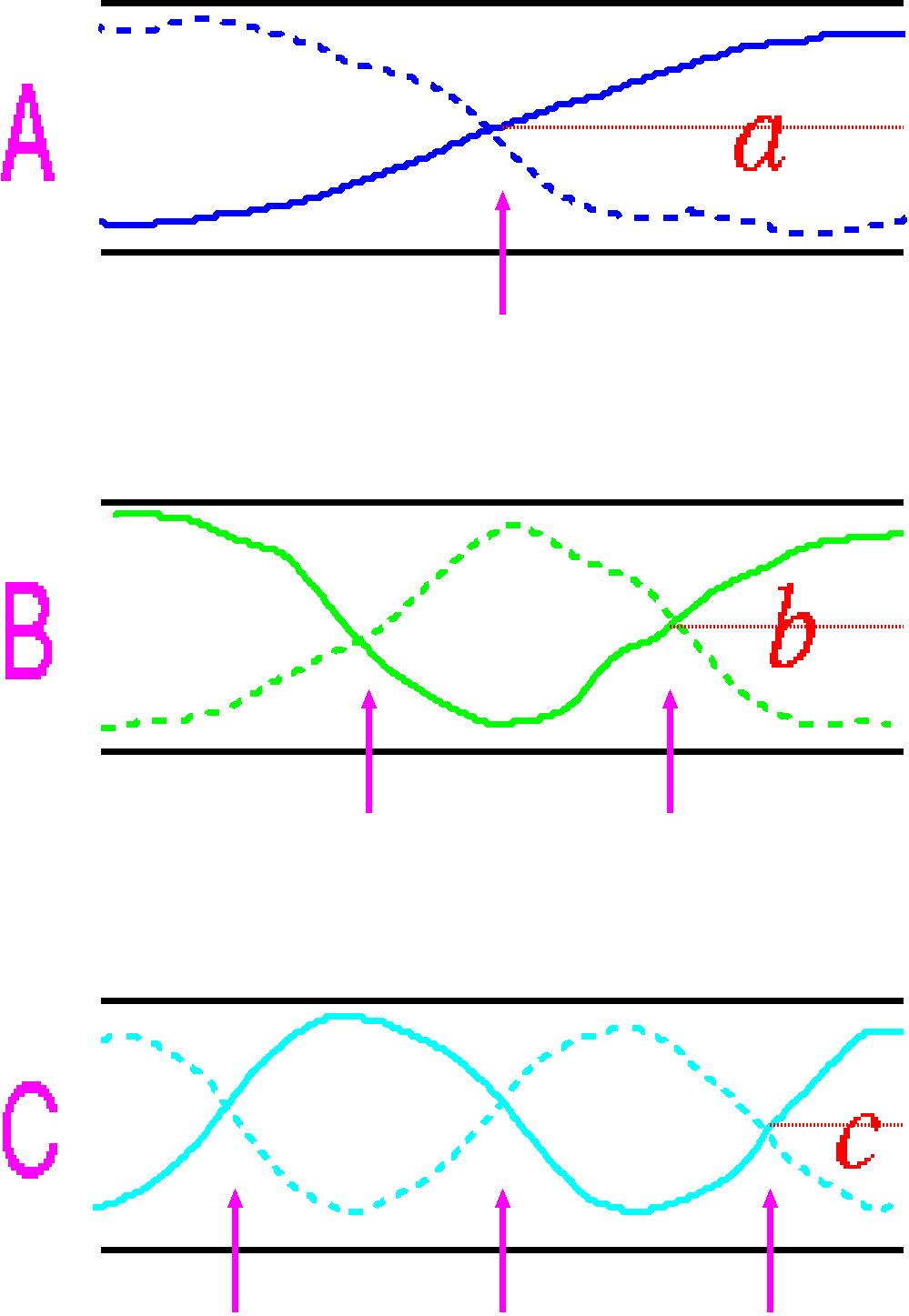図のように両端の空いた管に空気の振動を作るとします。
両端が空いているのですから両端の空気が自由に振動できることが
振動を決める条件です。
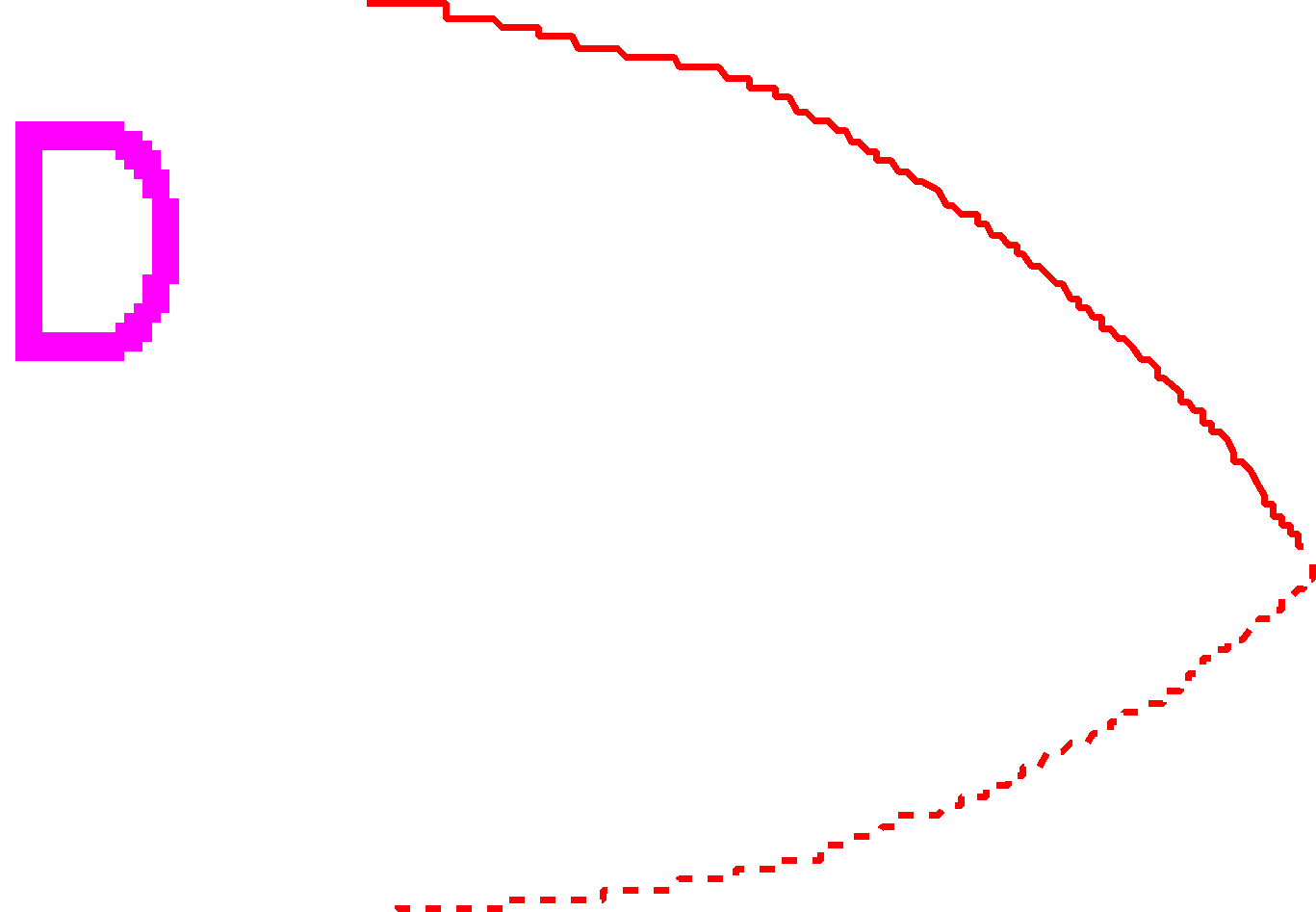今、Dに示されたさつまいも半分のような形を
半さつまと呼んで、
このパターンがA〜Cの中でどのように現れるか見ましょう。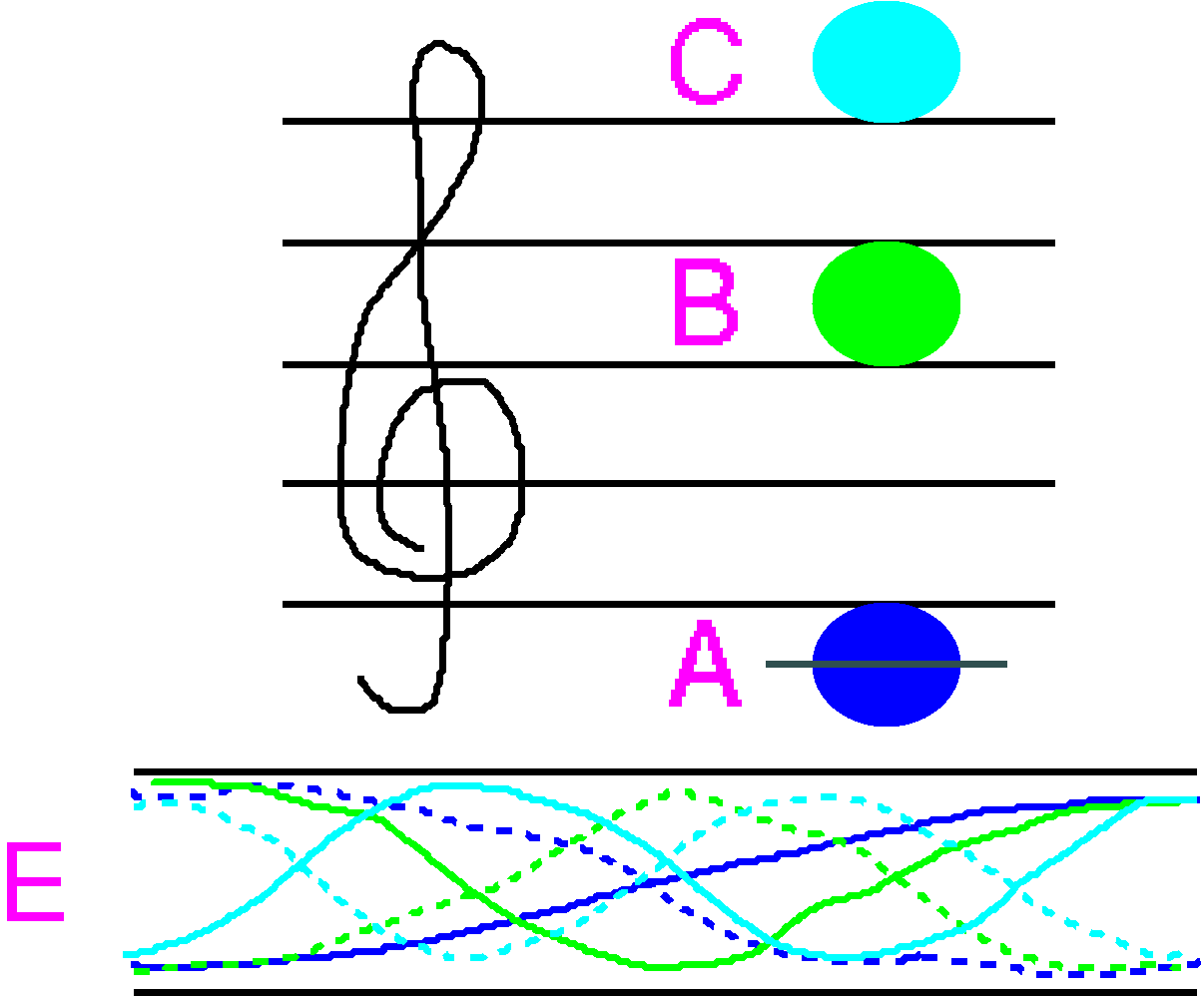
1.を用いれば、
AとB
の振動数の比は1:2であることから、
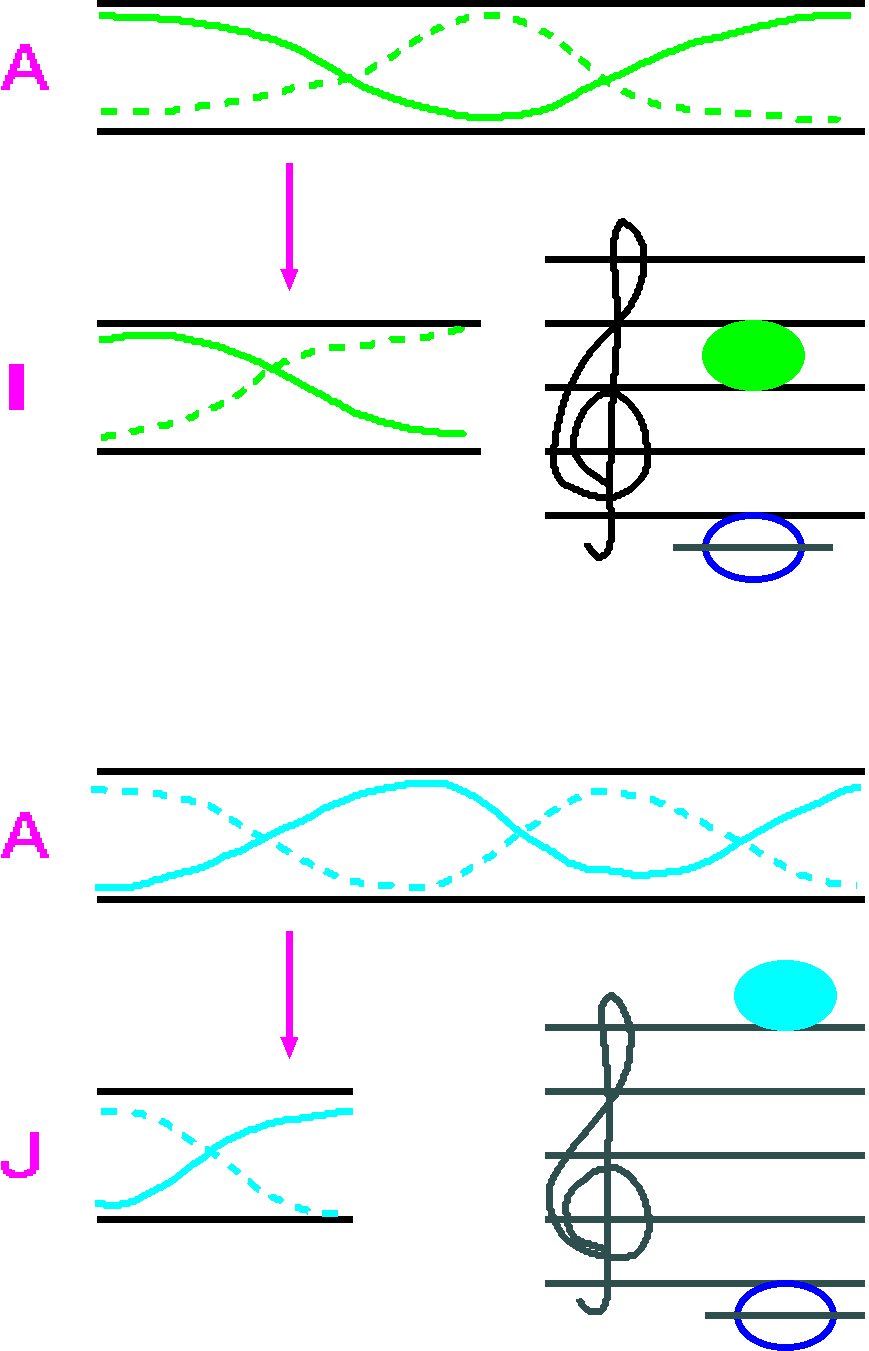この基音がドのパイプIは一オクターブ上のドの音に対応する振動数２倍の
倍音(ド)を持っています。
図の緑の振動
はこの振動数２倍の倍音の振動を示します。
この波が基音になるようなパイプIを作ると、
このパイプIは、
パイプAの一オクターブ上のドを鳴らすことになります。
長さはAの半分で、4フィートです。
次に、
11.Nasard 2 2/3'
というストップを入れてまた鍵盤の一番下のドを鳴らすと、
Nasardに属するパイプのうち、
2 2/3フィートの長さのパイプが
鳴ります。
これはソの音がなることが分かります。
2 2/3'や1 1/3'のように8'とオクターブの関係にない音を鳴らすストップを、
ミューテーションストップと言います。
ミューテーションストップは必ずオクターブストップと合わせて用いられます。
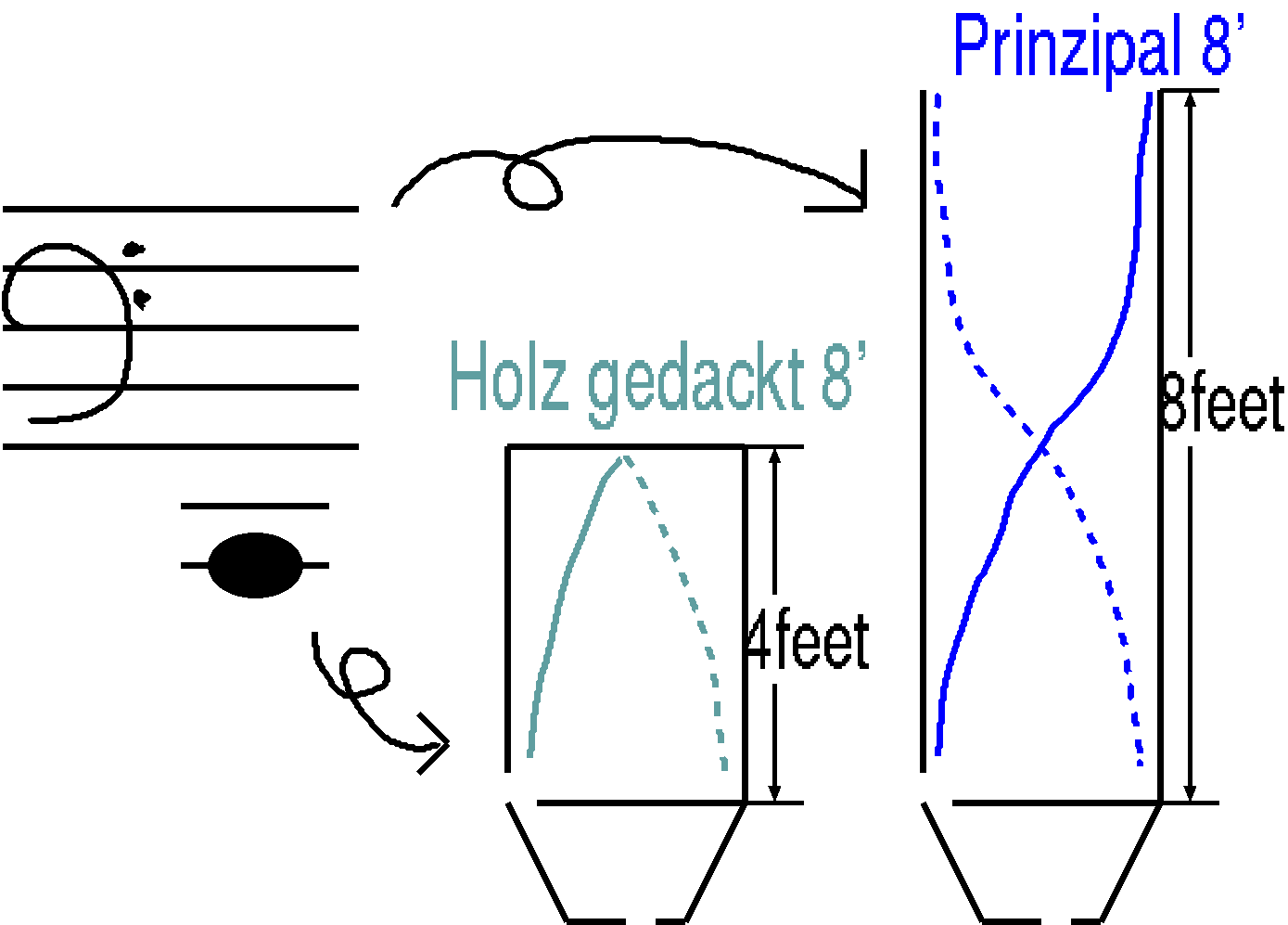さて、鍵盤の一番低いドの音が基音として、
Prinzipal 8'とHolz gedackt 8' のパイプで鳴っている様子を、
右図に示します。
両方とも同じドがなるのですが、
Prinzipal 8'のパイプが8フィートあるのに対して、
Holz gedackt 8'のパイプは4フィートしかありません。
これは、
「鍵盤の一番低いドの音を弾いた時に実際に鳴るパイプの長さを
ストップに記す」
という規則と矛盾しています。